Polar Coordinates
Table Of Contents
So far whenever we used coordinates we had a clear grid of 2 or 3 axes in which we could manipulate things and push them around. There were multiple spaces of those like object, world, screen, uv space and maybe more but the base rules were always the same most of the time. That pushing things to the right, pushes them to the right, up is up etc… This is called “cartesian coordinates”.
Now I want to introduce you to polar coordinates, how to convert to and from them and show you how to use them. While you manipulate polar coordinates, remember that not all rules from geometry in cartesian coordinates apply, but I encourage you to play with all ideas you have and see what happens.

Converting cartesian to polar coordinates 🔗︎
While in cartesian 2d space the 2 variables we use are the “right-ness” as well as the “up-ness”(or “down-ness” depending on context), in polar coordinates the 2 variables are the angle around the center and the distance from that center.
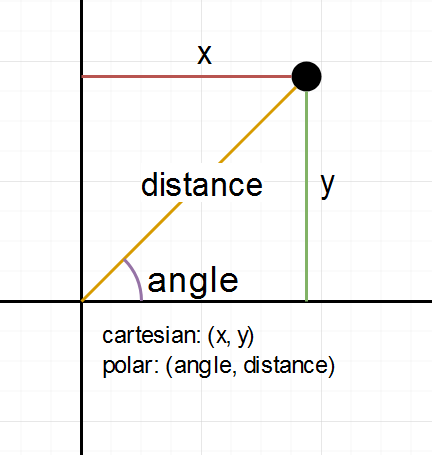
So we use the the atan2 to calculate the angle and calculate the length of the position for the distance and store it in a float2 (I used that because its convenient, you can also build your own struct for that if you prefer that). I put it in a function in a include file for reuse, but you can of course put the function in your shader file, or even do the calculations inline. As a small addition, I divided the angle by 2pi to make it go from -0.5 to 0.5, instead of -pi to pi, which is usually a more annoying number to work with.
#ifndef POLAR_COORDINATES
#define POLAR_COORDINATES
float2 toPolar(float2 cartesian){
float distance = length(cartesian);
float angle = atan2(cartesian.y, cartesian.x);
return float2(angle / UNITY_TWO_PI, distance);
}
#endif
Now we can continue by using that function in our shader. This is built on the basic shader tutorial shader, so nothing fancy is happening here.
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
//get polar coordinates
float2 uv = toPolar(i.uv);
return float4(frac(uv), 0, 1); //test output
}
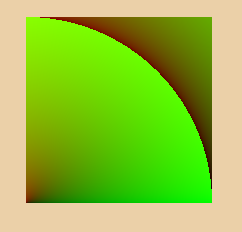
Here we can already see the distance going from 0 to 1 and beyond (since the diagnoal of a unit square is sqrt(2)). But we can also only see 1/4th of the circle. Thats because, as described earlier, we’re taking the angle around the “center”, and thats in the bottom right corner here. Luckily moving the center around in cartesian space is pretty easy, so lets just subtract 0.5 from each axis of the uvs before converting them. And because hlsl converts scalars automatically to vectors with each value set to the scalar, we can just write uv - 0.5. With this written, the space will be -0.5 to 0.5, so lets already multiply that by 2 to we get to -1 to 1 and get to see the whole 0-1 space.
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
//make input uvs centered and scaled to -1 to 1
i.uv -= 0.5;
i.uv *= 2;
//get polar coordinates
float2 uv = toPolar(i.uv);
return float4(frac(uv), 0, 1); //test output
}
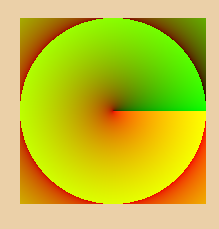
And now that we have those generated, we can just apply them to texture by using them as uv coordinates.
//sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;

The whole rotation is usually a bit much for a image and it gets stretched, but we can apply simple math onto those coordiantes like we’re used to. So lets just make it tile a few times for a better result. If we wanted to we could also apply a TRANSFORM_TEX macro here to apply the offset of the editor here.
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
//make input uvs centered and scaled to -1 to 1
i.uv -= 0.5;
i.uv *= 2;
//get polar coordinates
float2 uv = toPolar(i.uv);
//tile Image
uv.x *= 3;
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}

But as you can see theres sometimes a weird seam opposite of “0 degree”. Thats because there the coordinates jump from -1.5 to 1.5, they still sample the same point in a repeating texture, but tex2D uses partial derivatives internally which then in those pixels conclude that we’re watching the texture from very far away, and choose a lower mipmap level.
The “correct” solution to this is to calculate the mipmap level yourself and then pass it to tex2Dlod, but because thats too much for this tutorial, I’m just going to link this other excellent article to you on that: https://bgolus.medium.com/distinctive-derivative-differences-cce38d36797b.
Another solution is to move that seam to somewhere where its way less obvious. To do that here, we can only take the fractional part of the x coordinate of the output, since its from -0.5 to 0.5 by default, it will become 0 to 1, and the edge is at the start of the first image, at 0°.
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
//make input uvs centered and scaled to -1 to 1
i.uv -= 0.5;
i.uv *= 2;
//get polar coordinates
float2 uv = toPolar(i.uv);
//move discontinuity in coordinates to 0
uv.x = frac(uv.x);
//tile Image
uv.x *= 3;
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}

Using polar coordinates to manipulate cartesian coordinates 🔗︎
More often than as coordinates themselves, polar coordinates are used as a intermediate space to manipulate cartesian coordinates. That means we also need a function to turn polar coordinates into cartesian ones. To reverse the previous atan2, we use cos(angle) to get the cartesian x component and sin(angle) to get the y component. Since the outputs of the trigonometric functions return positions on a unit cicle with distance 1 from the center, recreating the distance from that center is a multiplication of that vector with the distance we stored in the second component of our polar float2. Do remember that we divided by 2 pi last time, so if you followed that, we also need to multiply by that now. And one other small thing, hlsl has a sincos function that does both calculations by using out parameters and I’m using that here, just so youre not confused.
float2 toCartesian(float2 polar){
float2 cartesian;
sincos(polar.x * UNITY_TWO_PI, cartesian.y, cartesian.x);
return cartesian * polar.y;
}
With this in our toolbelt, our fragment function should look like this:
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
float2 uv = i.uv - 0.5; //get centered uvs
uv = toPolar(uv); //make uvs polar
//manipulate uvs in polar space here
uv = toCartesian(uv); //convert uvs back to cartesian
uv += 0.5; //make uvs start in corner again
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}
As you see we don’t scale the UVs anymore, since we dont care if the edges are at distance 0.5 or distance 1, also the 0.5 we subtract at the start is added again since we still need the center to be in the corner for textures to be read correctly. With this, the result of your shader should look as if you’re never touching polar coordinates here since the conversion to and back should be relatively lossless.
If we now with this setup add to the polar x component, we rotate the image, and by multiplying the y component we can scale it (tho we could’ve done that without polar coordinates).
//manipulate uvs in polar space here
uv.x += _Time.y * 0.1;
uv.y *= 1 + sin(_Time.y * 3) * 0.2;

Though this is just uniform changes, you can get even more interresting results if you change the picture non-uniformly if you want to. For example just making the rotation dependent on the distance from the center (conveniently stored in the y component) creates a swirl pattern.
//manipulate uvs in polar space here
uv.x += sin(_Time.y) * uv.y * 1;

Theres many more things you can do with this using simple math (also look into using exponents(pow()) when playing with this), but this is where I leave you to your own devices and wish you lots of fun messing around.
Source 🔗︎
#ifndef POLAR_COORDINATES
#define POLAR_COORDINATES
float2 toPolar(float2 cartesian){
float distance = length(cartesian);
float angle = atan2(cartesian.y, cartesian.x);
return float2(angle / UNITY_TWO_PI, distance);
}
float2 toCartesian(float2 polar){
float2 cartesian;
sincos(polar.x * UNITY_TWO_PI, cartesian.y, cartesian.x);
return cartesian * polar.y;
}
#endif
Shader "Tutorial/053_Polar_Coordinates/Polar_UVs"{
//show values to edit in inspector
Properties{
_Color ("Tint", Color) = (0, 0, 0, 1)
_MainTex ("Texture", 2D) = "white" {}
}
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry" }
Pass{
CGPROGRAM
//include useful shader functions
#include "UnityCG.cginc"
#include "Polar.cginc"
//define vertex and fragment shader functions
#pragma vertex vert
#pragma fragment frag
//texture and transforms of the texture
sampler2D _MainTex;
float4 _MainTex_ST;
//tint of the texture
fixed4 _Color;
//the mesh data thats read by the vertex shader
struct appdata{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
//the data thats passed from the vertex to the fragment shader and interpolated by the rasterizer
struct v2f {
float4 position : SV_POSITION;
float2 uv : TEXCOORD0;
};
//the vertex shader function
v2f vert(appdata v){
v2f o;
//convert the vertex positions from object space to clip space so they can be rendered correctly
o.position = UnityObjectToClipPos(v.vertex);
//apply the texture transforms to the UV coordinates and pass them to the v2f struct
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
//make input uvs centered and scaled to -1 to 1
i.uv -= 0.5;
i.uv *= 2;
//get polar coordinates
float2 uv = toPolar(i.uv);
//move discontinuity in coordinates to 0
uv.x = frac(uv.x);
//tile Image
uv.x *= 3;
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}
ENDCG
}
}
Fallback "VertexLit"
}
Shader "Tutorial/053_Polar_Coordinates/Polar_Manipilation_1"{
//show values to edit in inspector
Properties{
_Color ("Tint", Color) = (0, 0, 0, 1)
_MainTex ("Texture", 2D) = "white" {}
}
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry" }
Pass{
CGPROGRAM
//include useful shader functions
#include "UnityCG.cginc"
#include "Polar.cginc"
//define vertex and fragment shader functions
#pragma vertex vert
#pragma fragment frag
//texture and transforms of the texture
sampler2D _MainTex;
float4 _MainTex_ST;
//tint of the texture
fixed4 _Color;
//the mesh data thats read by the vertex shader
struct appdata{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
//the data thats passed from the vertex to the fragment shader and interpolated by the rasterizer
struct v2f {
float4 position : SV_POSITION;
float2 uv : TEXCOORD0;
};
//the vertex shader function
v2f vert(appdata v){
v2f o;
//convert the vertex positions from object space to clip space so they can be rendered correctly
o.position = UnityObjectToClipPos(v.vertex);
//apply the texture transforms to the UV coordinates and pass them to the v2f struct
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//the fragment shader function
fixed4 frag (v2f i) : SV_Target {
float2 uv = i.uv - 0.5; //get centered uvs
uv = toPolar(uv); //make uvs polar
//manipulate uvs in polar space here
uv.x += _Time.y * 0.1;
uv.y *= 1 + sin(_Time.y * 3) * 0.2;
uv = toCartesian(uv); //convert uvs back to cartesian
uv += 0.5; //make uvs start in corner again
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}
ENDCG
}
}
Fallback "VertexLit"
}
Shader "Tutorial/053_Polar_Coordinates/Polar_Manipilation_2"{
//show values to edit in inspector
Properties{
_Color ("Tint", Color) = (0, 0, 0, 1)
_MainTex ("Texture", 2D) = "white" {}
}
SubShader{
//the material is completely non-transparent and is rendered at the same time as the other opaque geometry
Tags{ "RenderType"="Opaque" "Queue"="Geometry" }
Pass{
CGPROGRAM
//include useful shader functions
#include "UnityCG.cginc"
#include "Polar.cginc"
//define vertex and fragment shader functions
#pragma vertex vert
#pragma fragment frag
//texture and transforms of the texture
sampler2D _MainTex;
float4 _MainTex_ST;
//tint of the texture
fixed4 _Color;
//the mesh data thats read by the vertex shader
struct appdata{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
//the data thats passed from the vertex to the fragment shader and interpolated by the rasterizer
struct v2f {
float4 position : SV_POSITION;
float2 uv : TEXCOORD0;
};
//the vertex shader function
v2f vert(appdata v){
v2f o;
//convert the vertex positions from object space to clip space so they can be rendered correctly
o.position = UnityObjectToClipPos(v.vertex);
//apply the texture transforms to the UV coordinates and pass them to the v2f struct
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//the fragment shader function
fixed4 frag (v2f i) : SV_Target
{
float2 uv = i.uv - 0.5; //get centered uvs
uv = toPolar(uv); //make uvs polar
//manipulate uvs in polar space here
uv.x += sin(_Time.y) * uv.y * 1;
uv = toCartesian(uv); //convert uvs back to cartesian
uv += 0.5; //make uvs start in corner again
// sample the texture and apply tint
fixed4 col = tex2D(_MainTex, uv) * _Color;
//return the final color to be drawn on screen
return col;
}
ENDCG
}
}
Fallback "VertexLit"
}